
SL Paper 2
An arithmetic sequence has first term and common difference .
Given that the th term of the sequence is zero, find the value of .
Let denote the sum of the first terms of the sequence.
Find the maximum value of .
The temperature of water minutes after being poured into a cup can be modelled by where and are positive constants.
The water is initially boiling at . When , the temperature of the water is .
Show that .
Show that .
Find the temperature of the water when .
Sketch the graph of versus , clearly indicating any asymptotes with their equations and stating the coordinates of any points of intersection with the axes.
Find the time taken for the water to have a temperature of . Give your answer correct to the nearest second.
The model for the temperature of the water can also be expressed in the form for and is a positive constant.
Find the exact value of .
Consider the curves and for .
Find the -coordinates of the points of intersection of the two curves.
Find the area, , of the region enclosed by the two curves.
A function is given by .
The graph of the function intersects the graph of .
Expand the expression for .
Find .
Draw the graph of for and . Use a scale of 2 cm to represent 1 unit on the -axis and 1 cm to represent 5 units on the -axis.
Write down the coordinates of the point of intersection.
Consider the function .
The function has one local maximum at and one local minimum at .
Write down the -intercept of the graph of .
Sketch the graph of for −3 ≤ ≤ 3 and −4 ≤ ≤ 12.
Determine the range of for ≤ ≤ .
The following diagram shows a circle with centre and radius .
Points , and lie on the circumference of the circle.
Chord has length and radians.
Show that arc has length .
Show that .
Arc is twice the length of chord .
Find the value of .
Points and lie on opposite banks of a river, such that is the shortest distance across the river. Point represents the centre of a city which is located on the riverbank. , and .
The following diagram shows this information.
A boat travels at an average speed of . A bus travels along the straight road between and at an average speed of .
Find the travel time, in hours, from to given that
There is a point , which lies on the road from to , such that . The boat travels from to , and the bus travels from to .
An excursion involves renting the boat and the bus. The cost to rent the boat is per hour, and the cost to rent the bus is per hour.
the boat is taken from to , and the bus from to .
the boat travels directly to .
Find an expression, in terms of for the travel time , from to , passing through .
Find the value of so that is a minimum.
Write down the minimum value of .
Find the new value of so that the total cost to travel from to via is a minimum.
Write down the minimum total cost for this journey.
Let and , for .
Find .
Solve the equation .
Hence or otherwise, given that , find the value of .
Consider the curve y = 2x3 − 9x2 + 12x + 2, for −1 < x < 3
Sketch the curve for −1 < x < 3 and −2 < y < 12.
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.
State the name of the student who made an incorrect observation.
Find .
Show that the stationary points of the curve are at x = 1 and x = 2.
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.
Tommaso plans to compete in a regional bicycle race after he graduates, however he needs to buy a racing bicycle. He finds a bicycle that costs 1100 euro (EUR). Tommaso has 950 EUR and invests this money in an account that pays 5 % interest per year, compounded monthly.
The cost of the bicycle, , can be modelled by , where is the number of years since Tommaso invested his money.
Determine the amount that he will have in his account after 3 years. Give your answer correct to two decimal places.
Find the difference between the cost of the bicycle and the amount of money in Tommaso’s account after 3 years. Give your answer correct to two decimal places.
After complete months Tommaso will, for the first time, have enough money in his account to buy the bicycle.
Find the value of .
The following table shows the probability distribution of a discrete random variable , where and .
Show that .
Find the difference between the greatest possible expected value and the least possible expected value.
Let , for . The graph of passes through the point , where .
Find the value of .
The following diagram shows part of the graph of .
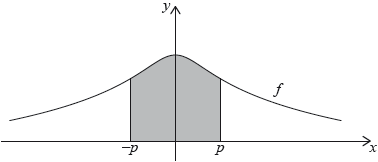
The region enclosed by the graph of , the -axis and the lines and is rotated 360° about the -axis. Find the volume of the solid formed.
Consider the function .
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
Sketch the graph of the function g (x) = 10x + 40 on the same axes.
Consider a function , such that , 0 ≤ ≤ 10, .
The function has a local maximum at the point (2, 21.8) , and a local minimum at (8, 10.2).
A second function is given by , 0 ≤ ≤ 10; , .
The function passes through the points (3, 2.5) and (6, 15.1).
Find the period of .
Find the value of .
Hence, find the value of (6).
Find the value of and the value of .
Find the value of for which the functions have the greatest difference.
The function is defined by , where .
For the graph of
The graphs of and intersect at and , where .
write down the equation of the vertical asymptote.
find the equation of the horizontal asymptote.
Find .
Using an algebraic approach, show that the graph of is obtained by a reflection of the graph of in the -axis followed by a reflection in the -axis.
Find the value of and the value of .
Hence, find the area enclosed by the graph of and the graph of .
The following diagram shows a semicircle with centre and radius . Points and lie on the circumference of the circle, such that and , where .
Given that the areas of the two shaded regions are equal, show that .
Hence determine the value of .
The height of water, in metres, in Dungeness harbour is modelled by the function , where is the number of hours after midnight, and and are constants, where and .
The following graph shows the height of the water for hours, starting at midnight.
The first high tide occurs at and the next high tide occurs hours later. Throughout the day, the height of the water fluctuates between and .
All heights are given correct to one decimal place.
Show that .
Find the value of .
Find the value of .
Find the smallest possible value of .
Find the height of the water at .
Determine the number of hours, over a 24-hour period, for which the tide is higher than metres.
The following table shows a probability distribution for the random variable , where .

A bag contains white and blue marbles, with at least three of each colour. Three marbles are drawn from the bag, without replacement. The number of blue marbles drawn is given by the random variable .
A game is played in which three marbles are drawn from the bag of ten marbles, without replacement. A player wins a prize if three white marbles are drawn.
Find .
Find .
Write down the probability of drawing three blue marbles.
Explain why the probability of drawing three white marbles is .
The bag contains a total of ten marbles of which are white. Find .
Jill plays the game nine times. Find the probability that she wins exactly two prizes.
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
Consider the function , where is a constant. Part of the graph of is shown below.

It is known that at the point where the tangent to the graph of is horizontal.
There are two other points on the graph of at which the tangent is horizontal.
Write down the -intercept of the graph.
Find .
Show that .
Find .
Write down the -coordinates of these two points;
Write down the intervals where the gradient of the graph of is positive.
Write down the range of .
Write down the number of possible solutions to the equation .
The equation , where , has four solutions. Find the possible values of .
All living plants contain an isotope of carbon called carbon-14. When a plant dies, the isotope decays so that the amount of carbon-14 present in the remains of the plant decreases. The time since the death of a plant can be determined by measuring the amount of carbon-14 still present in the remains.
The amount, , of carbon-14 present in a plant years after its death can be modelled by where and are positive constants.
At the time of death, a plant is defined to have units of carbon-14.
The time taken for half the original amount of carbon-14 to decay is known to be years.
Show that .
Show that .
Find, correct to the nearest years, the time taken after the plant’s death for of the carbon-14 to decay.
Consider the function
Find .
Solve .
The graph of has a local minimum at point .
Find the coordinates of .
Consider the function , where x > 0 and k is a constant.
The graph of the function passes through the point with coordinates (4 , 2).
P is the minimum point of the graph of f (x).
Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph.
A water container is made in the shape of a cylinder with internal height cm and internal base radius cm.

The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is .
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of .
Write down a formula for , the surface area to be coated.
Express this volume in .
Write down, in terms of and , an equation for the volume of this water container.
Show that .
Find .
Using your answer to part (e), find the value of which minimizes .
Find the value of this minimum area.
Find the least number of cans of water-resistant material that will coat the area in part (g).
Consider the lines and with respective equations
and .
A third line, , has gradient .
Find the point of intersection of and .
Write down a direction vector for .
passes through the intersection of and .
Write down a vector equation for .
Let for .
Sketch the graph of on the grid below.
Find the value of for which .
The quadratic equation , where , has real distinct roots.
Find the range of possible values for .
A scientist conducted a nine-week experiment on two plants, and , of the same species. He wanted to determine the effect of using a new plant fertilizer. Plant was given fertilizer regularly, while Plant was not.
The scientist found that the height of Plant , at time weeks can be modelled by the function , where .
The scientist found that the height of Plant , at time weeks can be modelled by the function , where .
Use the scientist’s models to find the initial height of
Plant .
Plant correct to three significant figures.
Find the values of when .
For , find the total amount of time when the rate of growth of Plant was greater than the rate of growth of Plant .
The functions and are defined for by and , where .
Find the range of .
Given that for all , determine the set of possible values for .
Consider the function , for .
Find the values of for which .
Sketch the graph of on the following grid.
SpeedWay airline flies from city to city . The flight time is normally distributed with a mean of minutes and a standard deviation of minutes.
A flight is considered late if it takes longer than minutes.
The flight is considered to be on time if it takes between and minutes. The probability that a flight is on time is .
During a week, SpeedWay has flights from city to city . The time taken for any flight is independent of the time taken by any other flight.
Calculate the probability a flight is not late.
Find the value of .
Calculate the probability that at least of these flights are on time.
Given that at least of these flights are on time, find the probability that exactly flights are on time.
SpeedWay increases the number of flights from city to city to flights each week, and improves their efficiency so that more flights are on time. The probability that at least flights are on time is .
A flight is chosen at random. Calculate the probability that it is on time.
A particle moves in a straight line such that its velocity, , at time seconds is given by .
Determine when the particle changes its direction of motion.
Find the times when the particle’s acceleration is .
Find the particle’s acceleration when its speed is at its greatest.
Consider the function ,
The function , , models the path of a river, as shown on the following map, where both axes represent distance and are measured in kilometres. On the same map, the location of a highway is defined by the function .
The origin, O(0, 0) , is the location of the centre of a town called Orangeton.
A straight footpath, , is built to connect the centre of Orangeton to the river at the point where .
Bridges are located where the highway crosses the river.
A straight road is built from the centre of Orangeton, due north, to connect the town to the highway.
Find the value of when .
Find the function, , that would define this footpath on the map.
State the domain of .
Find the coordinates of the bridges relative to the centre of Orangeton.
Find the distance from the centre of Orangeton to the point at which the road meets the highway.
This straight road crosses the highway and then carries on due north.
State whether the straight road will ever cross the river. Justify your answer.
Let , for x > 0.
The k th maximum point on the graph of f has x-coordinate xk where .
Given that xk + 1 = xk + a, find a.
Hence find the value of n such that .
OAB is a sector of the circle with centre O and radius , as shown in the following diagram.
The angle AOB is radians, where .
The point C lies on OA and OA is perpendicular to BC.
Show that .
Find the area of triangle OBC in terms of and θ.
Given that the area of triangle OBC is of the area of sector OAB, find θ.
Let and .
The graphs of and intersect at and , where .
Find the value of and of .
Hence, find the area of the region enclosed by the graphs of and .
Let , and .
Find .
Let be a point on the graph of . The tangent to the graph of at is parallel to the graph of .
Find the -coordinate of .
Consider the function defined by for .
The graph of and the line intersect at point .
The line has a gradient of and is a tangent to the graph of at the point .
The shaded region is enclosed by the graph of and the lines and .
Find the -coordinate of .
Find the exact coordinates of .
Show that the equation of is .
Find the -coordinate of the point where intersects the line .
Hence, find the area of .
The line is tangent to the graphs of both and the inverse function .
Find the shaded area enclosed by the graphs of and and the line .
Let and , for .
The graph of can be obtained from the graph of by two transformations:
Let , for . The following diagram shows the graph of and the line .

The graph of intersects the graph of at two points. These points have coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of ;
Write down the value of ;
Write down the value of .
Find .
Hence, find the area of the region enclosed by the graphs of and .
Let be the vertical distance from a point on the graph of to the line . There is a point on the graph of where is a maximum.
Find the coordinates of P, where .
Gemma and Kaia started working for different companies on January 1st 2011.
Gemma’s starting annual salary was , and her annual salary increases on January 1st each year after 2011.
Kaia’s annual salary is based on a yearly performance review. Her salary for the years 2011, 2013, 2014, 2018, and 2022 is shown in the following table.
Find Gemma’s annual salary for the year 2021, to the nearest dollar.
Assuming Kaia’s annual salary can be approximately modelled by the equation , show that Kaia had a higher salary than Gemma in the year 2021, according to the model.
A rocket is travelling in a straight line, with an initial velocity of m s−1. It accelerates to a new velocity of m s−1 in two stages.
During the first stage its acceleration, m s−2, after seconds is given by , where .
The first stage continues for seconds until the velocity of the rocket reaches m s−1.
Find an expression for the velocity, m s−1, of the rocket during the first stage.
Find the distance that the rocket travels during the first stage.
During the second stage, the rocket accelerates at a constant rate. The distance which the rocket travels during the second stage is the same as the distance it travels during the first stage.
Find the total time taken for the two stages.
Let and , for .
Show that .
On the following grid, sketch the graph of , for .

The equation has exactly two solutions, for . Find the possible values of .
Let , for .
For the graph of , find the -intercept.
Hence or otherwise, write down .
The following diagram shows the graph of a function , for .
The points and lie on the graph of . There is a minimum point at .
Let .
Write down the range of .
Write down the domain of .
A discrete random variable, , has the following probability distribution:
Show that .
Find the value of , giving a reason for your answer.
Hence, find .
Let for .
Write down the equation of the horizontal asymptote to the graph of f.
Let f(x) = ln x − 5x , for x > 0 .
Solve f '(x) = f "(x).